一般化線形モデルに関して情報の整理を試みます。理解が怪しいので後日追記予定。
一般化線形モデル
【結論】 モデル内のどこかに線形予測子をもつ統計モデルのことです。

係数βj と変数X を乗じた各特徴量の総和を求める上記のZを「線形予測子」と呼び、一般化線形モデルにおいてはモデル内のどこかに必ず含まれます。
一般線形モデルの特徴
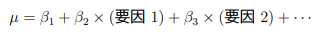
・目的変数yが正規分布に従う、すなわち誤差(実測値-推計値)が正規分布であることを仮定
・μ = z の形でモデルが表現される
一般化線形モデルの特徴

・一般化線形モデルは目的変数μに様々な関数を適用できるという特徴がある。例えば上記は、μにlog link関数を適用した log(μ) = z という式の両辺にexp() した形だが問題なく推計することができる。
・パラメータは最尤推定法によって計算される
一般化線形モデル(GLM)を作るのに必要なパーツ
コードをイメージしてからだと理解が簡単だと思う。
model = glm(target ~ . ,
family = Gamma(link= "log"),
data = df)
summary(model)① family
確率分布や誤差構造と呼ばれる。実測値yはどのような確率分布に従うと考えられるのか。実測値yの分布を見て判断するのが一般的。実測値と予測値の誤差を偏らせることで曲線を表現できる。
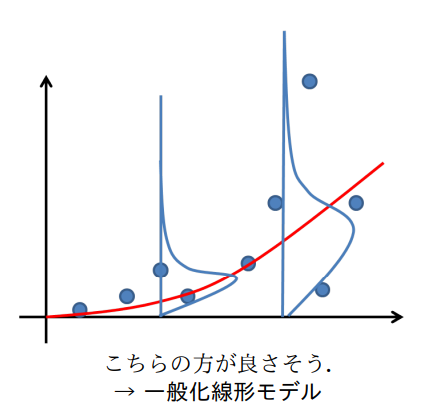
http://ibis.t.u-tokyo.ac.jp/suzuki/lecture/2015/dataanalysis/L4.pdf
② link関数
trainデータYとpredictデータYが同一の分布ではない場合を考える。
例えばロジスティック回帰の場合
・学習データYは二値変数
・predictデータYはp(Y=1) すなわち Y=1である確率 を求めたいことが多い
このような場合、trainデータyとpredictデータyをリンクさせるロジット変換などの計算ロジックが必要であり、リンク関数とよぶ。
③ 線形予測子
前述の説明におけるZ であり、指定の仕方は通常の回帰分析と変わらない
family とlink関数の対応表

https://multivariate-statistics.com/2021/03/06/r-programming-generalized-linear-model/
リンク関数
logit:二値変数 → 0~1の連続変数(≒確率)として扱うことができるようになる
probit:二値変数 → 0~1の連続変数(≒確率)として扱うことができるようになる
→ ほぼ同じ役割だが誤差項がロジスティック分布 / 正規分布 に従うという考え方が異なる
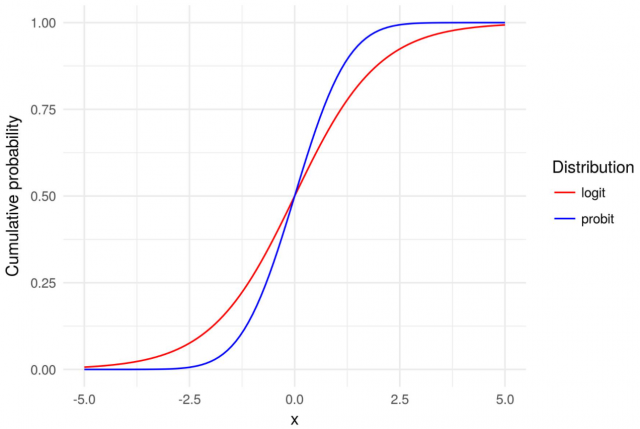
https://vitalflux.com/logit-vs-probit-models-differences-examples/
log:対数線形モデル、結果解釈としてはexp()で元のスケールに戻した後、1単位上がると●倍
identity:線形予測子 z = 推定値 *変換しない
確率分布
・binomial:二項分布
・gaussian:正規分布、ガウスマルコフモデルとも。
・gamma:ガンマ分布
・poisson:ポアソン分布
他のあまり使わない分布はおいおい覚えていけばいいのかなと思っています。。。
参考
講義のーと : データ解析のための統計モデリング
データ解析第四回「線形回帰分析の拡張:一般化線形モデル」
【R言語】一般化線形モデル 関数glmの使いかた
井出草平の研究ノート ガンマ分布のglm()モデリング[R]


コメント