決定係数に関する情報をまとめています。本ページは断りなく更新する場合があります。
決定係数の考え方
決定係数(R2値)という名前はなんとなく知っているものの、その考え方を説明するのって意外と難しいですよね。まず本章では決定係数の考え方について私なりの言葉で整理を試みます。詳細な数式や定義等は割愛しています。
【結論】 決定係数は回帰モデルが単純モデルと比べて、誤差の大きさがどの程度改善されたかを示す値
順に考え方を整理します。
そもそも「良い」回帰モデルとは何でしょうか。一般に線形回帰モデルは最小二乗法という考え方で「予測値と実績値の残差(≒誤差)」を最小化するように傾きや切片を求めます。誤差が小さいモデルのほうが与えられた値をより良く予測できているという考え方です。(当たり前ですが)。最小化しようとしているこの「誤差の大きさ」に注目することで良い回帰モデルが判断できそうです。
実測値yiと予測値y^の差を取ることで「誤差の大きさ」を求めることができます。
ただし、その数値だけでは一般的に良い値なのかどうかの判断ができません。元の数値の規模感に大きく依存するからです。そこでyの値の平均をただ取っただけの単純モデルを考えます。単純モデルの誤差の大きさを基準値に置くことで、回帰モデルによって誤差の大きさが相対的にどの程度改善されたか、比率で確認できるようになります。(この誤差がどの程度改善されたかのことを「説明力」と表現している本もありますが分かりづらい気がします。知らない単語を知らない単語で説明されても…となりがち)
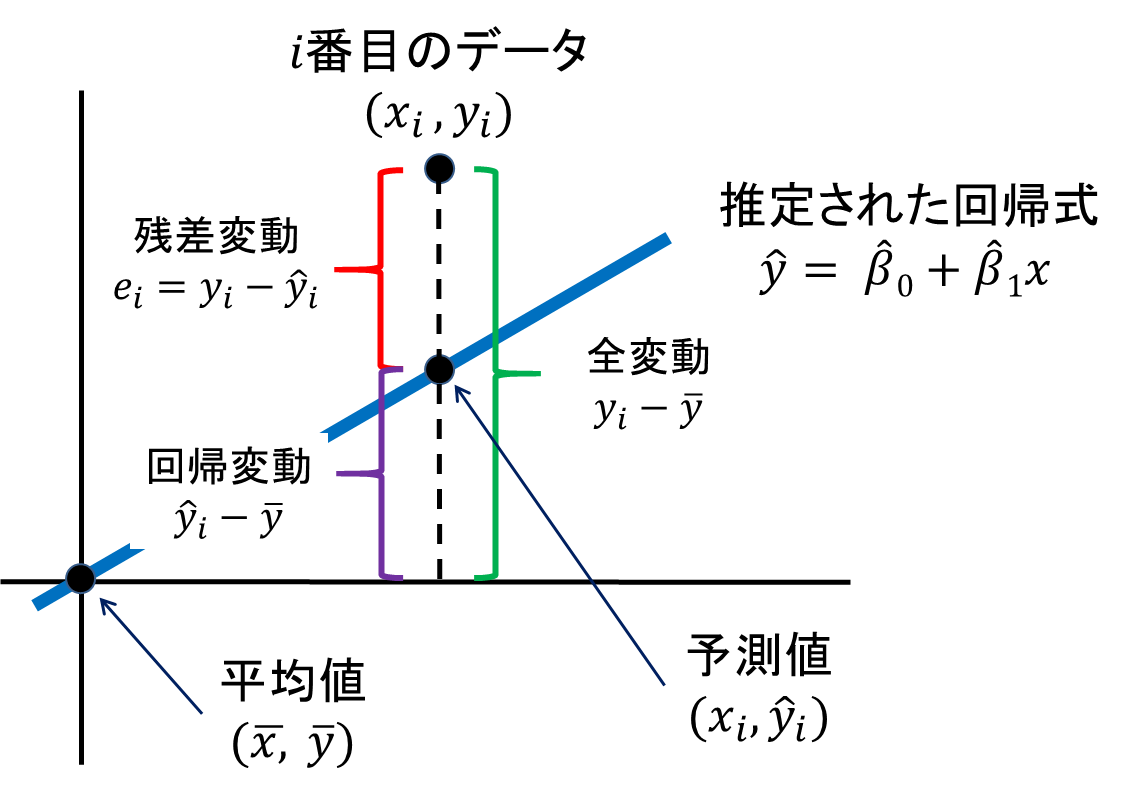
この段階で下記のグラフを元に一度用語を整理します。このグラフにおいてX,Y軸の十字は0を示していない点に注意が必要です。この十字が先ほどの「単純モデル」を示します。その単純モデルから回帰モデルの予測値までの距離を「回帰変動」(回帰分析によって生じた変動)、単純モデルから実測値までの距離を「全変動」、回帰モデルから実測値までの距離を「残差変動」(回帰分析の残差によって生じた変動)と表現しています。このとき定義より全変動 = 回帰変動 + 残差変動となります。
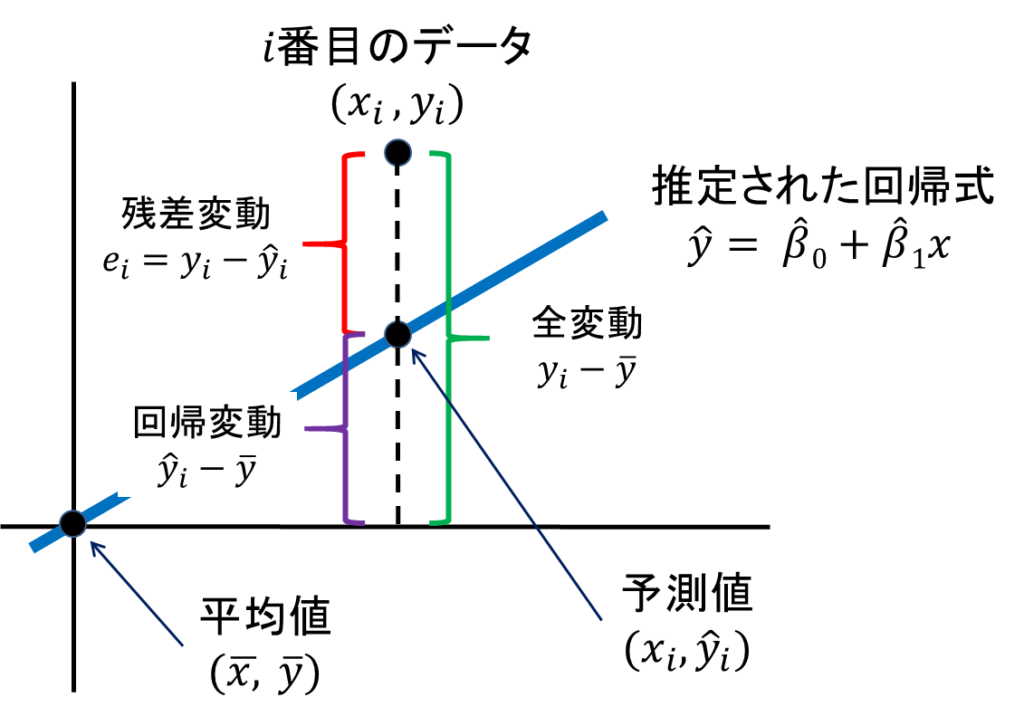
誤差の大きさがどの程度改善されたかを示す決定係数を求める数式は以下です。
右側の式に注目すると、
yi – yi^ = 実測値 – 回帰モデルの予測値 = 回帰モデルの誤差 = 残差変動
yi – y– = 実績値 – 単純モデルの予測値 = 単純モデルの誤差 = 全変動
を示すため、単純に回帰モデルと単純モデルの誤差の比率を見ているだけということが分かります。
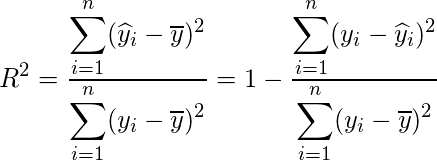
決定係数と推定値の関係性
ポイントは今回の重回帰分析が「説明」「因果」のどちらを目的とするかです。
・説明:なぜ今のこの値になっているのか要素を積み重ねていってwhyを説明する
・因果:treatがoutcomeに与える因果の部分にのみ興味がある
“因果”の効果推定は、計量経済学などでよく用いられる不偏性、一致性、有効性の検討であり、係数の量的な評価となる。“説明”の文脈で重回帰分析を用いる場合は、決定係数などのモデルの予測性能を評価することに主眼がある。
「学習成果」論再考 ─EBPMと因果推論を手がかりに─
https://www.juaa.or.jp/upload/files/publication/other/%E3%80%8C%E5%AD%A6%E7%BF%92%E6%88%90%E6%9E%9C%E3%80%8D%E8%AB%96%E5%86%8D%E8%80%83%E3%80%80.pdf
同様の、因果では係数に注目し決定係数は重視しないというニュアンスは以下でも見られます。
Btreatment 以外のパラメータの推定値も得られます。(中略)しかし、効果検証のための回帰分析では Btreatment 以外の推定結果には基本的に興味がなく、それらのパラメータが本当の効果を表すようになる努力も行わないため、介入効果を示すパラメータ以外については無視することになります。
効果検証入門 (2020 安井) p48 効果検証のための回帰分析で行わないこと
因果推論の文脈においてはBtreatment の係数およびそのp値に注目します。p値は「介入の効果 = 0」の確率であり、p値 <5%の場合は介入効果は0ではなかったようだと判断します。
予測能力や手元のデータに対する説明能力を(中略)考慮していない理由は「モデルのデータに対する説明能力や、未知のサンプルに対する予測能力を高めることが、”効果検証において有用である”という保証にはならない」という点にあります。
効果検証入門 (2020 安井) p84 回帰分析に関する様々な議論 予測と効果推定
上記の文における「元のデータに対する説明能力」を「決定係数」に読み替えても問題ないかと思います。「決定係数を高めること」と「Btreatment の値の正確性」は関係がないということです。その例としてRCTが紹介されていました。RCTはランダムに割り振られるためバイアスが非常に小さい(正確性の高い)分析結果を得られる一方、RCTの結果を回帰分析しても決定係数は低いことが予想されます。ただ、モデルの目的変数に対する説明能力を向上させることは、推定値の標準偏差を小さくすることに繋がるため、介入効果の検証としても無価値でないと結論付けられています。
決定係数に関するよくある疑問
Q. 決定係数が低いにも関わらず、p値で有意差が見られるとき、効果があると考えていいんだっけ?
データの個数が極端に多くなった場合には、係数や決定係数が小さく、説明変数と被説明変数の間に関係がありそうに見えなくても、係数のt検定の結果、t値やp値が有意となることがあり得る。これは、データの個数が増えたため推計の精度が上がり、係数がゼロに近い値であっても、それがゼロであるとはいえないという意味でt値(及びp値)が有意となるからである。(中略)結論的にいえば、②ではデータの個数が非常に多かったためである。
参議院 調査情報担当室 回帰分析におけるt値とp値の意味について
https://www.sangiin.go.jp/japanese/annai/chousa/keizai_prism/backnumber/r02pdf/202019202.pdf
A. サンプル数が多いだけで統計上有意差はあるが注意が必要な状態です。基本的には「なし」で考えたほうが良さそうです。
Q. 「説明」を目的とする重回帰分析の活用イメージが知りたい。
A. どの特徴量が目的変数に影響を与えているのか確認したい場合、
高精度な予測モデルを作りたい場合(Yを正確に予測したい場合) などが考えられそうです。
前者に関しては標準化偏回帰係数を求める必要があるのでご留意ください。
他の変数と比較してどの説明変数が目的変数に影響を与えているのか知りたい場合は、データを事前に標準化してから回帰分析を実行します。データを標準化することで変数間の尺度がそろうため、説明変数同士の比較が可能となります。標準化されたデータの偏回帰係数のことを標準化偏回帰係数と呼び、通常の偏回帰係数と区別します。
NTTコムオンライン回帰分析の具体例から活用方法を解説
https://www.nttcoms.com/service/research/dataanalysis/regression-analysis/
Q. 目的変数に効く特徴量が知りたいときは、特徴量ごとに単回帰分析を繰り返したらよいのでは?
A. 交絡因子(処置変数、目的変数の両方に影響を持つ因子)が存在する場合に、そこを統制(モデルに含める)しないと推計が大きくズレてしまいます。単回帰分析を繰り返しても推定値自体が大きくズレている懸念があるため、大きさの比較はできません。ある変数が交絡因子かどうか分からない場合は基本的にモデルに組み込む方向で考えればよいです。
不要な変数をモデルに取り入れることには、不偏性という点からは大きな問題はないが、標準誤差に悪影響が出る恐れはある.
統計的因果推論の理論と実装 (2022 高橋) p101 不要な変数をモデルに取り入れる問題
その他、決定係数に関する疑問点や誤り等ありましたらツイッターまでコメント頂けますと幸いです。

コメント