統計的因果推論を勉強するとしばしば多重共線性は基本的に考慮しなくてよいという記載がある。同時に回帰分析を学習したことがある人だと「あれ、それっていいんだっけ?」と思うのは自然なことだと思う。ここでは因果推論における回帰分析の前提条件を確認後、実際に多重共線性のあるサンプルデータを生成して不偏に推定ができるのかシミュレーションしてみた。
回帰モデルを使った因果推論の4つの前提条件
まず回帰分析で因果推論をするときの4つの前提条件を見てみよう。
・\(X_1 や X_2\) と \(y\) が線形性を持つ
・交絡因子の漏れがない
・残差の等分散性
・完全な多重共線性がない
1. \(X_1 や X_2\) と \(y\) が線形性を持つ
「パラメータにおける線形性」と表現されることも。\(X_1 や X_2\) と \(y\) の分布は線形性を持つ必要があるという仮定。重回帰の場合は成分プラス残差プロット(Component + Residual Plot:別名 partial residual plot)を使用して確認し、線形性が確認できない場合は変数変換を行う。
library(car)
model_pattern1 = lm(y ~ x1 + x2 , data = df)
crPlots(model_pattern1)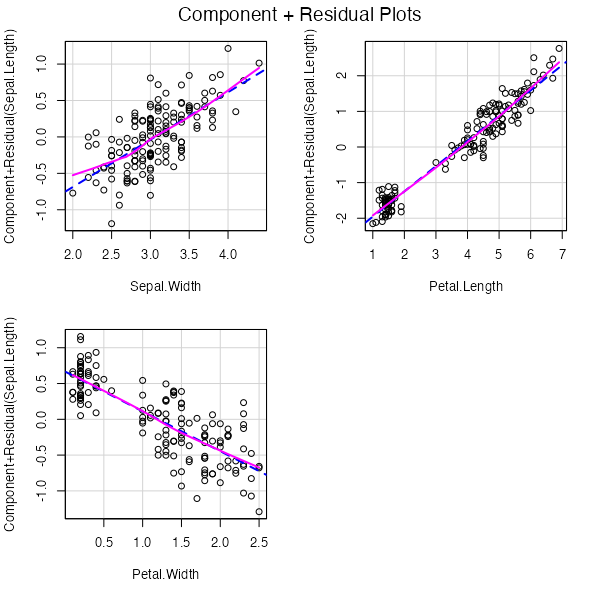
2.交絡因子の漏れがない
交絡因子が統制されていない場合、推計値が不安定になるため、必ずモデルに含める必要がある。ただし、現実問題として交絡因子の漏れを判断する術はないので、ここでは交絡因子の抜け漏れがないと仮定して無理やり進むことにする。
3.残差の等分散性
アウトカムYが大きくなるにつれて誤差も大きくなってしまう状況は×という話。
(例.売上1万円のときは±5000円で予測できても売上10億円だと±5000円の予測は難しい)
等分散の仮定を満たしていなくても各係数の点推定値に影響はないものの、その推定誤差が変わってきてくる。対処法としては主に以下の2つ。
- 反復再重み付け最小二乗法(Iteratively Reweighted Least Squares, IRLS):通常どおり推定した残差をもとに、各対象者への重み付けを計算し、それを使って再度残差を計算し、またそれをもとに重み付けを更新し…という方法
- 一般化推定方程式(Generalized Estimating Equations, GEE):IRLSを発展させ、対象者間で誤差の相関関係を考慮した方法
4. 完全な多重共線性がないこと
因果推論においては多重共線性は基本的に問題視しないと言われている。
共変量の間に多重共線性が起きていても、特に問題視する必要はないのである。それどころか、共変量のうちの片方を取り除いてしまうと、交絡を取り除き切ることができなくなってしまう
統計的因果推論の理論と実践 (高橋2022)
それどころか、強い多重共線性の共変量でも取り除いた場合は交絡を除去しきれなくなるのでむしろ残す必要があるらしい。
唯一問題となるのが「完全な多重共線性」がある場合。完全な多重共線性とは共変量同士が完全に1:1の対応関係ができている場合を指し、例えば Aさんの日本での給料と ドルに換算した場合の値というデータがあった場合、この2つは本質的に同じ情報を持っているのでどちらか削除する必要がある。
処置変数\(X_1\)と共変量\(X_i\)で多重共線性があった場合、推定自体は不偏に行うことができるが標準誤差が大きくなることからp値が大きくなり、信頼区間も広くなる。
処置変数\(X_1\)と関係のない共変量\(X_a\)、\(X_b\)間で多重共線性があった場合、多重共線性の影響で\(X_a\)、\(X_b\)推計値が不安定になるが本来的にそこは求めたい値ではなく、\(X_1\)には影響がほぼないため、特に問題視しない。
実際に試してみる
多重共線性があっても推定自体は不偏に行うことができるのは本当か確かめてみる。以下で実際に強い多重共線性を持つデータセットを生成し、回帰分析を実行した。
library(car)
set.seed(99)
x1 = rnorm(100, 10, 1) # 共変量1:treatにもoutcome(=y)にも影響を与える交絡因子
x2 = rnorm(100, 10, 2) # 共変量2:outcome(=y)にのみ影響を与える
treat = x1 * 2 + rnorm(100,10,0.001) # 処置効果を見たい変数
e = rnorm(100, 0, 1) # 誤差項
y = 1*x1 + 2*x2 + 5*treat + e # 最終的なモデル式
df = data.frame(y,x1,x2,treat)
model = lm(y ~ x1 + x2 +treat,data = df)
vif(model)
> vif(model)
x1 x2 treat
2.673454e+06 1.008768e+00 2.673468e+06
summary(model)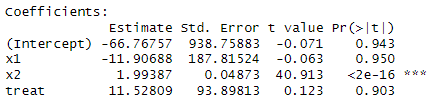
あれ?全然違う値になった。念のためパラメータにおける線形性を確認してみる。
crPlots(model)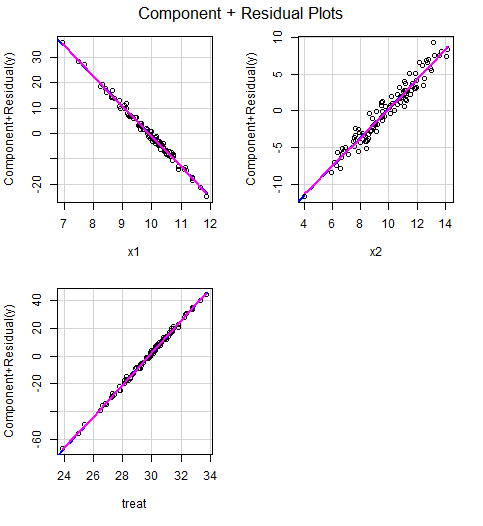
問題なく線形性があるように見える。10あれば高い相関があると言われるVIFが 2.673468e+06(267万) というふざけた数値だからか?数値変更して再トライしてみる。
set.seed(99)
x1 = rnorm(100, 10, 1)
x2 = rnorm(100, 10, 2)
treat = x1 * 2 + rnorm(100,10,0.5) # X1との相関が高すぎたので分散を0.01→0.5に変更
e = rnorm(100, 0, 1)
y = 1*x1 + 2*x2 + 5*treat + e
df = data.frame(y,x1,x2,treat)
model = lm(y ~ x1 + x2 +treat,data = df)
vif(model)
> vif(model)
x1 x2 treat
12.801867 1.008768 12.832078
summary(model)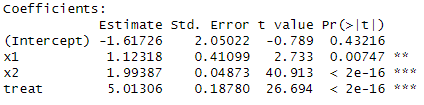
お、欲しかった「5」という値が出た。vifが10程度のときはうまくいくようだ。とはいえvifによってtreatの推計ができるできないが変わると判断するのはまだ早計かも。1万パターンシミュレーションしてみた。
df = data.frame() # 空のdata.frameを用意する
counter = 0
for(i in 1:10000) {
set.seed(99)
x1 = rnorm(100, 10, 1)
x2 = rnorm(100, 10, 2)
treat = x1 * 2 + rnorm(100,10,0.001 * i) # この誤差の部分を色々と試すことでvifを変動させる
e = rnorm(100, 0, 1)
y = 1*x1 + 2*x2 + 5*treat + e
tmp = data.frame(y,x1,x2,treat)
model = lm(y ~ x1 + x2 +treat,data = tmp)
tmp2 = data.frame(v = 0.001 * i,
vif = vif(model) %>% max(),
estimate = model$coefficients[4],
confint_low = confint(model)[4,1],
confint_high = confint(model)[4,2]) # 出力結果を保存
df = rbind(df,tmp2) # 空のdata.frameに順に入れていく
counter = counter +1 # 進行度合いの把握用
print(counter)
}
# 可視化
ggplot(data =df ,mapping = aes(x=vif,y=estimate))+
geom_line()+
geom_hline(yintercept = 5)+
theme_classic()
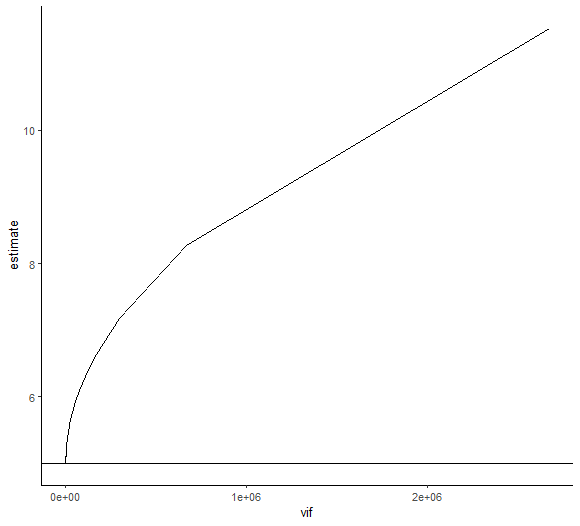
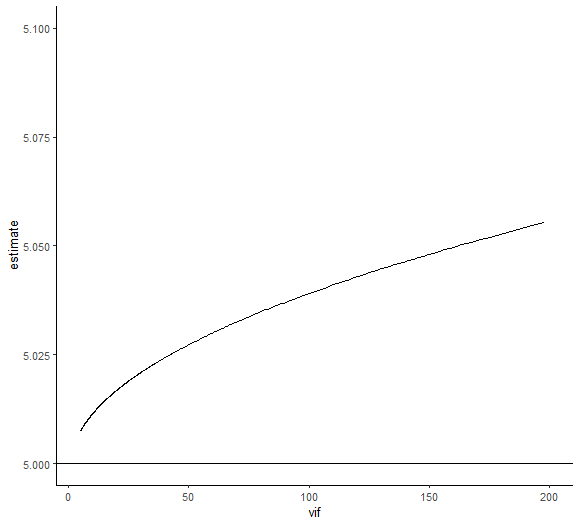
左側が10000件試した結果。vifが上がるほどestimateの値が5という真値からどんどんズレていることが分かる。一方で右側がvif200未満かつestimate5.1未満の範囲に注目して切り抜いた図。vifが100あっても5.05と精度高く予測できている。vifが現実的な値であれば、多少高くてもestimate自体は問題なく推計できるということか。信頼区間はどうなんだろう。
ggplot(data =df)+
geom_pointrange(mapping = aes(x = vif,y = estimate,ymin =confint_low,ymax=confint_high))+
geom_hline(yintercept = 5)+
theme_classic()+
xlim(0,200)+
ylim(3,7)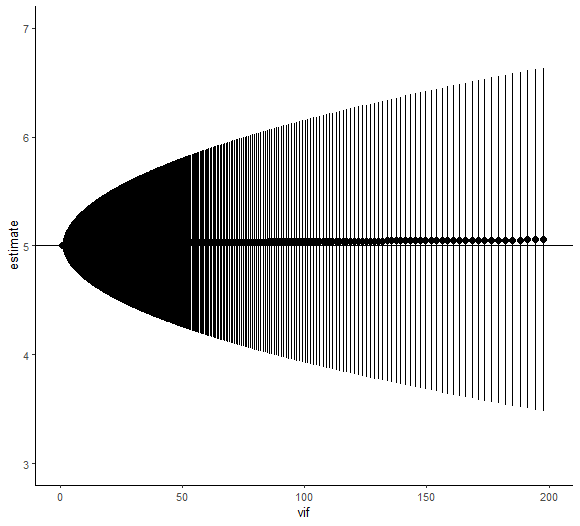
vifが上がるほど信頼区間が広がっていく様子が分かる。ただ推定値(黒い●)はほぼ5付近であり、vifの上昇による影響をほぼ受けていないみたい。これは先の説明の「推定値は不偏に行えるが信頼区間が広がる」と考えると良さそう。
結論
VIFがよほど大きくなければestimateは真値に近い値になるようだった。
因果推論文脈においてよく言われる
多重共線性は気にしなくてよい
は言い換えれば
(現実的な値であれば) 多重共線性は気にしなくてよい
ということで理解しておくのが良さそう。
(結構ガバガバなシミュレーションだから詳しい人が見たら怒られそうだなぁと思いつつ…)


コメント